The Third Dimension

Now that we've gotten comfortable with transformations and basic drawing, let's look at how to work in 3D. If you explore some of the ci::gl namespace you'll spot some 3D cousins to gl::drawSolidCircle() - functions like gl::drawSphere() and gl::drawCube().

Let's see what happens if we simply swap in a call to gl::drawCube():

#include "cinder/app/App.h"
#include "cinder/app/RendererGl.h"
#include "cinder/gl/gl.h"

using namespace ci;
using namespace ci::app;

class BasicApp : public App {
  public:
	void draw() override;
};

void BasicApp::draw()
{
	gl::clear();
	
	// this will work, right?
	gl::drawCube( vec3(), vec3( 2 ) );
}

CINDER_APP( BasicApp, RendererGl )

Not quite what we'd hoped for. As you may recall, by default Cinder sets things up so that the coordinate systems match the app::Window pixel-for-pixel in 2D. However to draw in 3D we'll need to create a 3D coordinate system. The simplest way is to use a CameraPersp. This class allows us to create a virtual camera, specifying the point at which the camera is positioned, and the point that it is looking at. To position a CameraPersp at (3, 3, 3) and have it look at the origin (0, 0, 0), we'll use CameraPersp::lookAt( vec3( 3 ), vec3( 0 ) ).

A very valuable tool for understanding the CameraPersp class is the sample by the same name:

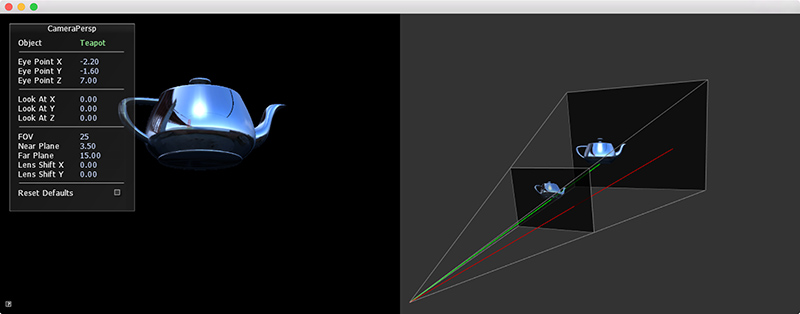
After creating a CameraPersp, we need to set our matrices to match. In addition to the Model matrix discussed previously, Cinder maintains a View matrix and a Projection matrix. While the Model matrix is used to position an object in the world (more formally the object to world-space transformation), the View matrix is used to position our virtual "eye" in the world (the world to view-space transformation). We are manipulating a View matrix when we call routines like CameraPersp::lookAt(), thereby modifying the position and orientation by which the virtual world is viewed. Other properties affect how 3D is projected onto the 2D image plane or screen. These include the aspect ratio, field-of-view and clipping planes. Together, this data represents a Projection matrix. By calling gl::setMatrices() and passing a CameraPersp, Cinder's OpenGL View and Projection matrices are set.

void BasicApp::draw()
{
	gl::clear();

	CameraPersp cam;
	cam.lookAt( vec3( 3, 3, 3 ), vec3( 0 ) );
	gl::setMatrices( cam );

	gl::drawCube( vec3(), vec3( 2 ) );
}

While it lacks the shading that we normally associate with 3D, the result is the distinctive outline of a cube. We'll look at how to improve its look soon, and some of the details of how these matrices interact with convenience methods like gl::drawCube() will become apparent as well. In the meantime, a helpful debugging technique can be to print these matrices to the console. For this purpose we can use gl::getModelMatrix(), gl::getViewMatrix(), and gl::getProjectionMatrix().

console() << gl::getProjectionMatrix() << std::endl;

[[    1.299,    0.000,    0.000,    0.000]
 [    0.000,    1.732,    0.000,    0.000]
 [    0.000,    0.000,   -1.002,   -2.002]
 [    0.000,    0.000,   -1.000,    0.000]]

Let's add some simple Lambert shading to the example. We'll get into shaders in more detail later, but for the time being we'll use gl::ShaderDef. This class allows us to easily create basic shaders without writing any GLSL shader code. In order to make this the active shader, we call gl::getStockShader(), and then bind() the result. Again, we'll go into much more depth with shaders in the upcoming sections, so don't get too hung up on this yet.

#include "cinder/gl/Shader.h"
…

void BasicApp::draw()
{
	gl::clear();

	CameraPersp cam;
	cam.lookAt( vec3( 3, 3, 3 ), vec3( 0 ) );
	gl::setMatrices( cam );

	auto lambert = gl::ShaderDef().lambert();
	auto shader = gl::getStockShader( lambert );
	shader->bind();
	// draw sphere at the origin, radius 1
	gl::drawSphere( vec3(), 1.0f );
}

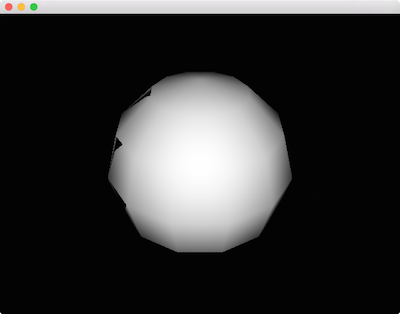
This is a start, but has a couple of visible problems. We've switched to gl::drawSphere(), but the sphere itself looks pretty low resolution. Perhaps more problematic though, there are mysterious black triangles on its left side. Fortunately the solution for both of these problems are straightforward:

void BasicApp::draw()
{
	gl::clear();
	// turn on z-buffering
	gl::enableDepthRead();
	gl::enableDepthWrite();

	CameraPersp cam;
	cam.lookAt( vec3( 3, 3, 3 ), vec3( 0 ) );
	gl::setMatrices( cam );

	auto lambert = gl::ShaderDef().lambert();
	auto shader = gl::getStockShader( lambert );
	shader->bind();
	gl::drawSphere( vec3(), 1.0f, 40 );
}

Much better. First, our black triangle artifact is gone, because we've enabled the Z-Buffer (also known as the depth buffer). If you're not familiar, Z-Buffering is the standard technique for preventing fragments from drawing on top of each other incorrectly. It uses a per-pixel depth value to ensure that no pixel draws on top of a pixel it is "behind." Various effects can be achieved by variously enabling and disabling depth buffer read and write, as well as its testing function, which we won't be exploring here. Just keep in mind that in the general 3D case, we want to call gl::enableDepthRead() and gl::enableDepthWrite(). In addition this example provides the optional third parameter to gl::drawSphere() which increases the subdivisions to 40, resulting in a much smoother appearance.

3D Transforms

Let's extend the use of transformations into 3D:

void BasicApp::draw()
{
	gl::clear();
	gl::enableDepthRead();
	gl::enableDepthWrite();

	CameraPersp cam;
	cam.lookAt( vec3( 5, 2, 5 ), vec3( 0, 1, 0 ) );
	gl::setMatrices( cam );

	auto lambert = gl::ShaderDef().lambert().color();
	auto shader = gl::getStockShader( lambert );
	shader->bind();
	
	int numSpheres = 64;
	float maxAngle = M_PI * 7;
	float spiralRadius = 1;
	float height = 3;
	
	for( int s = 0; s < numSpheres; ++s ) {
		float rel = s / (float)numSpheres;
		float angle = rel * maxAngle;
		float y = rel * height;
		float r = rel * spiralRadius * spiralRadius;
		vec3 offset( r * cos( angle ), y, r * sin( angle ) );
		
		gl::pushModelMatrix();
		gl::translate( offset );
		gl::color( Color( CM_HSV, rel, 1, 1 ) );
		gl::drawSphere( vec3(), 0.1f, 30 );
		gl::popModelMatrix();
	}
}

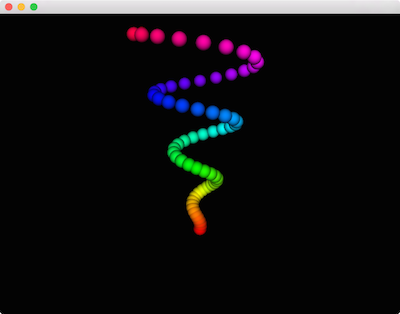
One change this snippet highlights is the addition of .color() on the Lambert shader. It should otherwise be familiar. Let's look at introducing a bit of animation now.

void BasicApp::draw()
{
	gl::clear();
	gl::enableDepthRead();
	gl::enableDepthWrite();

	CameraPersp cam;
	cam.lookAt( vec3( 3, 4.5, 4.5 ), vec3( 0, 1, 0 ) );
	gl::setMatrices( cam );

	auto lambert = gl::ShaderDef().lambert().color();
	auto shader = gl::getStockShader( lambert );
	shader->bind();
	
	int numSpheres = 64;
	float maxAngle = M_PI * 7;
	float spiralRadius = 1;
	float height = 2;
	float anim = getElapsedFrames() / 30.0f;

	for( int s = 0; s < numSpheres; ++s ) {
		float rel = s / (float)numSpheres;
		float angle = rel * maxAngle;
		float y = fabs( cos( rel * M_PI + anim ) ) * height;
		float r = rel * spiralRadius;
		vec3 offset( r * cos( angle ), y / 2, r * sin( angle ) );
		
		gl::pushModelMatrix();
		gl::translate( offset );
		gl::scale( vec3( 0.05f, y, 0.05f ) );
		gl::color( Color( CM_HSV, rel, 1, 1 ) );
		gl::drawCube( vec3(), vec3( 1 ) );
		gl::popModelMatrix();
	}
}

Here we're creating the anim variable as a function of getElapsedFrames() and then using it to govern the scale of the boxes.

In the next section we'll graduate from the GL convenience methods and look at using gl::Batch to improve performance.