RULE 3: ALIGNMENT

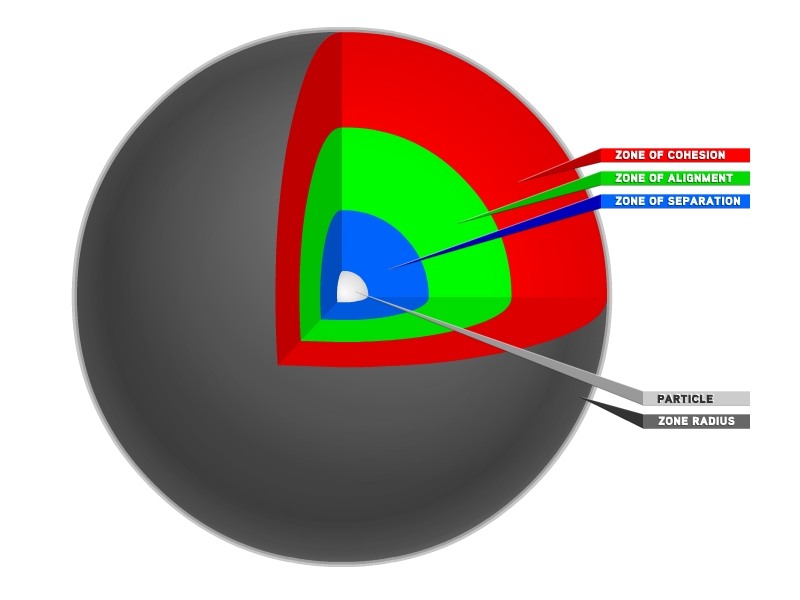
It is time to introduce the third rule. As you recall, the first rule was an act of separation. If an object gets too crowded, it tries to move away from its neighbors. The second rule is an act of cohesion. If an object moves too far away, it tries to move towards its neighbors. These two rules alone are enough to make some interesting flocking simulations. The resulting look is not too dissimilar from how tiny winged insects behave: a seemingly chaotic wandering but still exhibiting some group behavior.

Rule 3 gets us to a more familiar and less random looking system. This rule says that if a neighbor is not too far away or too close, then emulate its velocity. Or in other words, move like your neighbors move.

Let's bring back the applyForce() method to see what changes were made to accommodate this new third zone.

void ParticleController::applyForce( float zoneRadiusSqrd, float lowThresh, float highThresh  )
        {
            for( list::iterator p1 = mParticles.begin(); p1 != mParticles.end(); ++p1 ) {
                list::iterator p2 = p1;
                for( ++p2; p2 != mParticles.end(); ++p2 ) {
                    Vec3f dir = p1->mPos - p2->mPos;
                    float distSqrd = dir.lengthSquared();

                    if( distSqrd < zoneRadiusSqrd ) { // If the neighbor is within the zone radius...
                        float percent = distSqrd/zoneRadiusSqrd;

                        if( percent < lowThresh ) { // ... and is within the lower threshold limits, separate...
                            float F = ( lowThresh/percent - 1.0f ) * 0.01f;
                            dir = dir.normalize() * F;
                            p1->mAcc += dir;
                            p2->mAcc -= dir;
                        }
                        else if( percent < highThresh ) { // ... else if it is within the higher threshold limits, align...
                            float threshDelta = highThresh - lowThresh;
                            float adjustedPercent = ( percent - lowThresh )/threshDelta;
                            float F = ( 0.5f - cos( adjustedPercent * M_PI * 2.0f ) * 0.5f + 0.5f ) * 0.01f;
                            p1->mAcc += p2->mVel.normalized() * F;
                            p2->mAcc += p1->mVel.normalized() * F;
                        }
                        else { // ... else, attract.
                            float threshDelta = 1.0f - highThresh;
                            float adjustedPercent = ( percent - highThresh )/threshDelta;
                            float F = ( 0.5f - cos( adjustedPercent * M_PI * 2.0f ) * 0.5f + 0.5f ) * 0.01f;
                            dir = dir.normalize() * F;
                            p1->mAcc -= dir;
                            p2->mAcc += dir;
                        }
                    }
                }
            }
        }

The orientation force is similar to what we are doing with the cohesive force. We normalize the Particle's position within the range which it finds itself, and then use that normalized position to find the position along the inverted cosine. Here is what our curve now looks like.

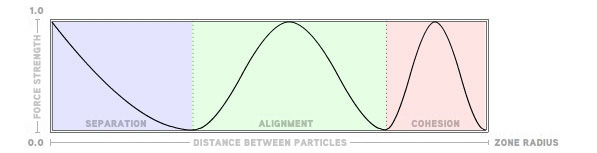
There is another difference with the alignment force that is different from separation and cohesion forces. The alignment force doesn't care about the vector between the interacting particles. It is more interested in the other particle's current velocity. This is why we are referencing mVel of the other Particle instead of manipulating the dir vector between Particles. If you are not too close to me and not too far away from me, I want to start moving in the direction you are moving. This simple process is what helps to create group flocking behavior in a random collection of particles with random starting positions and random starting velocities.

When you run the Chapter 4 Flocking app, you will get a random mess of particles but after a couple seconds, groups will begin to form.

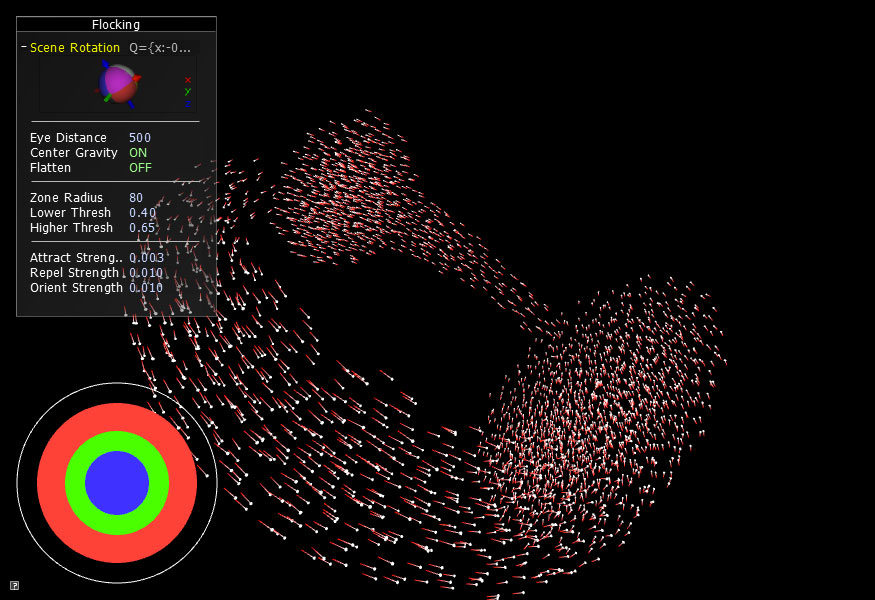
It is not uncommon for the flocking Particles to begin to form vortices that are characteristic of many species of fish. In the image below, thousands of sardines swim into a tight formation known as a bait ball which is a type of shoaling.

Photo credit: Erwin Poliakoff (Flickr:epddiver)

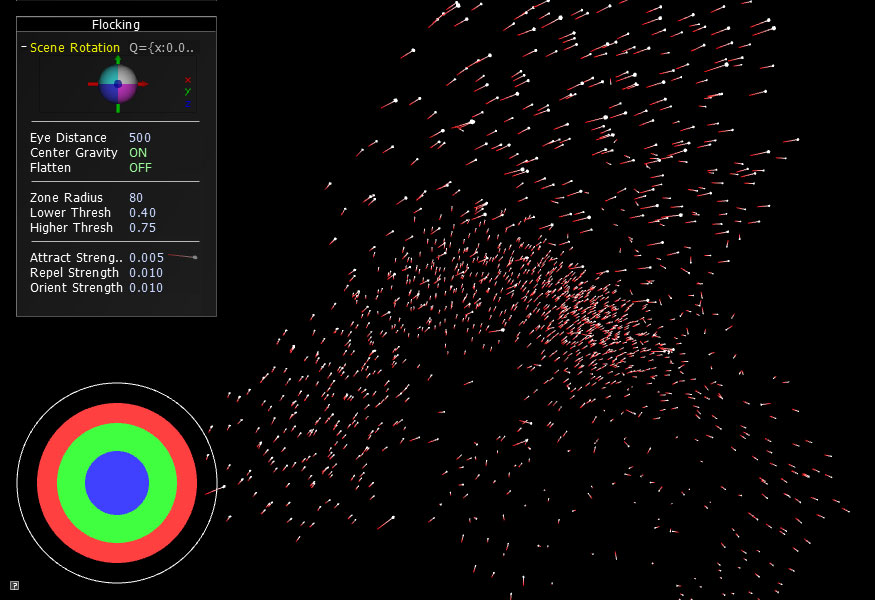
There you have it. A fairly basic 3D flocking particle simulation. In Flocking Chapter 5, we are going to show different ways you can improve the behavior of the flocking and also add in a few predators.