RULE 4: EVASION


No longer is our virtual world a peaceful place where objects can flock freely and travel in a blissful nirvana of vortices and happy neighbors wanting for nothing. Now we show them life can be cruel.

4527424956_9962a3d979_o.jpg

Photo Credit: Bo Pardau (Flickr:bodiver)

Rule 4 is simple enough. If you see a predator coming, run away and fast. We have created a Predator class that is nearly a duplicate of our Particle class (which is the prey in our simulation). In fact, these two classes are so similar many of you more experienced coders will probably be thinking “Why not make a flocking class and subclass the Predators and Prey&rdquo? We definitely should consider this option but for the sake of readability, we are going to leave this as an exercise for the reader.

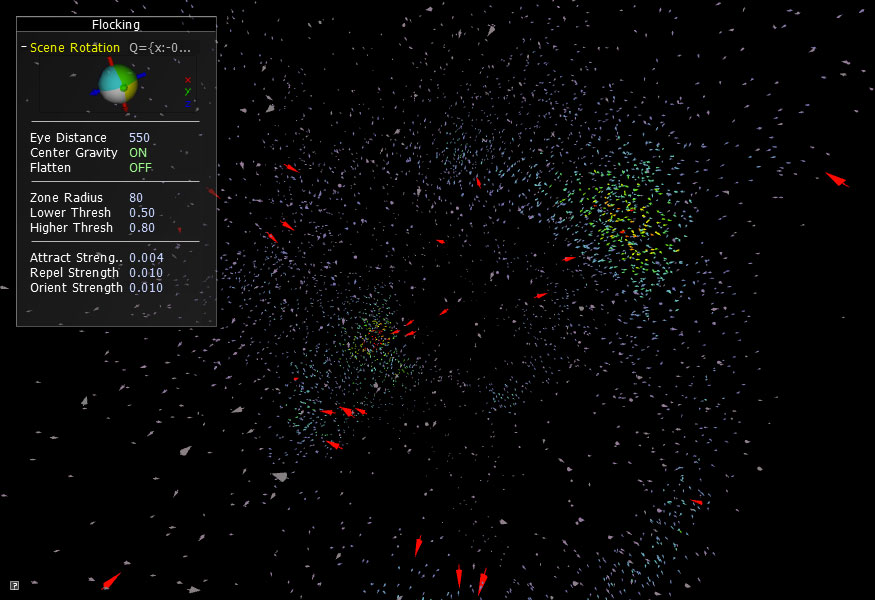
chapter5b.jpg



The Predators will behave like the other objects in our virtual world. They avoid collisions and loneliness and also try to travel in packs. However, they are also drawn towards the largest clump of prey within their zone radius (which we have defined to be three times the size of the prey's zones). Our Particle prey continue to abide by their three rules but whenever they sense a nearby Predator, they move away from the Predator's location.

float eatDistSqrd = 10.0f;
float predatorZoneRadiusSqrd = zoneRadiusSqrd * 3.0f;
for( list::iterator predator = mPredators.begin(); predator != mPredators.end(); ++predator ) {
Vec3f dir = p1->mPos[0] - predator->mPos[0];
float distSqrd = dir.lengthSquared();
if( distSqrd < predatorZoneRadiusSqrd ){
if( distSqrd > eatDistSqrd ){
float F = ( predatorZoneRadiusSqrd/distSqrd - 1.0f ) * 0.1f;
p1->mFear += F * 0.1f;
dir = dir.normalized() * F;
p1->mAcc += dir;
predator->mAcc += dir;
} else {
p1->mIsDead = true;
predator->mIsHungry = false;
// predator->mHunger -= p1->mMass;
}
}
}


To apply the Predator response, we add another list iterator into the outer nested list of our applyForce() method (which is officially a poorly named method so it is now called applyForceToParticles() and the version for Predators is called applyForceToPredators() ). For every Particle, check its distance to every Predator. If that distance is small enough, the Particle is eaten (mIsDead = true) and it is removed from the mParticles list in the ParticleController::update() method. Additionally, set the Predator's hunger boolean to false. Or if we are dealing with a much larger Predator, you could create an mHunger float which increases with each passing frame. Every time the predator is successful at feeding, the mHunger amount decreases by an amount proportional to the size of the eaten prey.

chapter5a.jpg



If the distance to the Predator is greater than the eating distance but smaller than the 3x zone radius, this means flee. The Particle's acceleration vector is greatly influenced by the vector between Particle and Predator. Additionally, the Predator's acceleration vector is also affected similarly in order to give chase.

Since our Predators generally move faster than our Particles, we have added a fear variable. As the Predator nears, the Particle's mFear variable increases. This variable is then used to influence the Particle's maximum speed.

float maxSpeed = math<float>::min( mMaxSpeed + mFear, 5.0f );
float maxSpeedSqrd = maxSpeed * maxSpeed;


This doesn't mean the Particle will always outrun the Predator. There is still a cap to the maximum speed burst allowed, but the extra little bit should help prolong the Particle's life.

However, the Predator has a corresponding hunger variable. The more time that passes since the Predator last fed, the greater the Predator's max speed. To summarize: Predators normally outswim Particles. When a Particle is scared, it can outswim the Predator. However, if the Predator is hungry enough, it can outswim a frightened Particle.

CROWDING


In our flocking simulation, each Particle pays attention to all the neighbor Particles within a set distance. However, it is theorized that each bird in a flock would pay attention to a limited number of close neighbors. Estimates put this number between 5 and 10. We can fairly quickly simulate this limited neighbor influence theory by allowing each Particle to adjust its zone radius based on how crowded it feels.

float zoneRadiusSqrd = zoneRadius * p1->mCrowdFactor * zoneRadius * p2->mCrowdFactor;


Each Particle has its own crowd factor variable which is inversely related to how many neighbors it has. When iterating through the nested lists in applyForceToParticles(), we count the number of close neighbors for each Particle. We can then use that number to adjust the radius of influence for each Particle. We can easily show the how crowded each Particle is by adjusting the color we use to draw the Particle. If the Particle is very crowded, mCrowdFactor decreases and the color shifts to saturated red. If the Particle is very isolated, the mCrowdFactor increases and its color shifts to desaturated purple. This is a fairly straightforward way of giving each Particle its own personality. Though the rules governing the behavior of these Particles are global, the parameters can easily be individualized.

CURRENT


We are going to add one final element to our flocking code. It is time to reintroduce Perlin noise (which we discussed in Section 1: Chapter 4). If we are simulating birds, the Perlin noise can be tweaked to create a strong breeze. If we are simulating fish, the Perlin dfBm() method can help to facilitate the formation of vortices in our flocking agents.

float scale = 0.005f;
float multi = 0.1f;
p1->mAcc += mPerlin.dfBm( p1->mPos * scale ) * multi;


All we do is add in a Perlin influence based on the position of each Particle. After we create our Perlin instance and set our controlling variables, all we need is one line of code. Try commenting this line out and seeing if you can notice the difference. Also play around with the scale and multi variables to control the extent to which the Perlin can influence the Particles.

CONCLUSION


Flocking simulations are especially powerful because they allow even beginner programmers to appreciate the complex beauty that arises as a result of emergent behaviors. When you consider the controlled chaos of a flock of tens of thousands of starlings flying in near perfect synchrony, or a tightly packed bait ball of shoaling fish, it confuses the mind. How are they able to avoid collisions? How do they all seem to know when and where to turn? Viewed from a distance, it seems like it would be a near impossible task for a computer to simulate.

Starling Flock at the Vatican from Tim Stutts on Vimeo.



However, when you analyze the problem from inside the group and consider what any one individual is thinking, the problem becomes quite simple. I should avoid crashing into the others around me. I should move in the general direction of my neighbors. If I wander too far from the group, I could die. If I see a predator, I should flee. These are the four basic rules of flock/swarm/shoaling behavior.

The following video was made with the source code for this chapter.

1 vs. 35,000 from flight404 on Vimeo.


Further reading:

1.) Flocks, Herds, and Schools: A Distributed Behavioral Model by Craig Reynolds
2.) Steering Behaviors for Autonomous Characters by Craig Reynolds
3.) Wikipedia entry on Shoaling and Schooling
4.) Statistical Physics is for the Birds by Toni Feder

Back to index: Tutorial Index.